Имея формулы для определения деформаций и зная условия закрепления стержня, нетрудно определить угловые перемещения сечений стержня и построить эпюры этих перемещений. Если имеется вал (т.е. вращающийся стержень), у которого нет неподвижных сечений, то для построения эпюры угловых перемещений принимают какое-либо сечение за условно неподвижное.
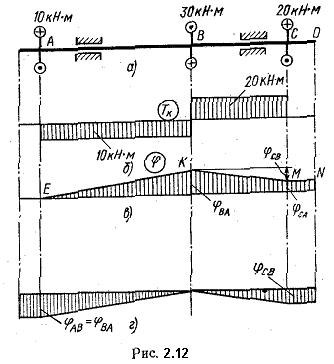
Рассмотрим конкретный пример (рис. 2.12, а). На рис. 2.12, б дана эпюра Тк.
Примем сечение в точке А за условно неподвижное. Определим поворот сечения В по отношению к сечению А.
По формуле (2.20) (см. здесь) найдем
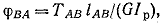
где ТАВ - крутящий момент на участке АВ; lАВ - длина участка АВ.
Примем следующее правило знаков для углов поворота сечений: углы 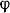 будем считать положительными, когда сечение поворачивается (если смотреть вдоль оси справа налево) против часовой стрелки. В данном случае будем считать положительными, когда сечение поворачивается (если смотреть вдоль оси справа налево) против часовой стрелки. В данном случае 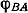 будет положительным. В принятом масштабе отложим ординату будет положительным. В принятом масштабе отложим ординату 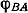 (рис. 2.12, в). Полученную точку К соединяем прямой точкой Е, так как на участке АВ углы изменяются по закону прямой линии [см. формулу 2.19, в которую абсцисса сечения z входит в первой степени]. Вычислим теперь угол поворота сечения С по отношению к сечению В. Учитывая принятое правило знаков для углов закручивания, получаем (рис. 2.12, в). Полученную точку К соединяем прямой точкой Е, так как на участке АВ углы изменяются по закону прямой линии [см. формулу 2.19, в которую абсцисса сечения z входит в первой степени]. Вычислим теперь угол поворота сечения С по отношению к сечению В. Учитывая принятое правило знаков для углов закручивания, получаем
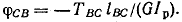
Так как сечение В не неподвижное, то угол поворота сечения С по отношению к сечению А равен
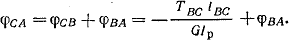
Угол закручивания 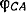 может получиться положительным, отрицательным и, в частном случае, равным нулю. может получиться положительным, отрицательным и, в частном случае, равным нулю.
Предположим, что в данном случае угол 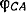 получился положительным. Тогда, отложив эту величину в принятом масштабе вверх от эпюры, получим точку М. Соединяя точку М с точкой К, получим графмк углов закручивания получился положительным. Тогда, отложив эту величину в принятом масштабе вверх от эпюры, получим точку М. Соединяя точку М с точкой К, получим графмк углов закручивания 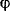 на участке ВС. На участке CD скручивания не происходит, так как крутящие моменты на этом участке равны нулю, поэтому там все сечения поворачиваются на столько же, на сколько поворачивается сечение С. Участок MN эпюры на участке ВС. На участке CD скручивания не происходит, так как крутящие моменты на этом участке равны нулю, поэтому там все сечения поворачиваются на столько же, на сколько поворачивается сечение С. Участок MN эпюры 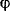 здесь горизонтален. Читателю предлагается убедиться, что если принять за неподвижное сечение В, то эпюра углов закручивания будет иметь вид, представленный на рис. 2.12, г. здесь горизонтален. Читателю предлагается убедиться, что если принять за неподвижное сечение В, то эпюра углов закручивания будет иметь вид, представленный на рис. 2.12, г.
Пример 2.1. Определить диаметр стального вала, вращающегося с угловой скоростью W = 100 рад/с и передающего мощность N = 100 кВт. Допускаемо напряжение 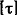 = 40 МПа, допускаемый угол закручивания = 40 МПа, допускаемый угол закручивания 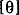 = 0,5 град/м, G = 80000 МПа. = 0,5 град/м, G = 80000 МПа.
Решение. Момент передаваемый валом, определяется по формуле
T = N/W = 100 000 / 100 = 1000 Н * м
Крутящий момент во всех поперечных сечениях вала одинаков
Tк = Т = 1000 Н * м = 1 кН * м = 0,001 МН * м.
Диаметр вала по прочности определяем по формуле (2.15)
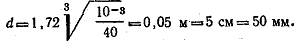
По формуле (2.24) определяем диаметр вала из условия жесткости
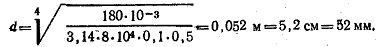
Диаметр вала в данном случае определяется из условия жесткости и должен быть принят равным d = 52 мм.
Пример 2.2. Подобрать размеры сечения трубчатого вала, передающего момент Т = 6 кН * м, при соотношении диаметров с = d/D = 0,8 и допускаемом напряжении 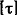 = 60 МПа. Сравнить вес этого трубчатого вала с валом равной прочности сплошного сечения. = 60 МПа. Сравнить вес этого трубчатого вала с валом равной прочности сплошного сечения.
Ответ. Размеры трубчатого вала: D = 9,52 см, d = 7,62 см. Плошадь сечения Ат = 25,9 квадратных см. Диаметр вала сплошного сечения d1 = 8 см. Площадь сечения Ас = 50,2 квадратных см. Масса трубчатого вала составляет 51% от массы сплошного вала.
Источник: http://sopromat.org | 





