При изменении угла 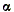 величины Ix1, Iy1 и Ix1y1 изменяются. Найдем значение угла, при котором Ix1 и Iy1 имеют экстремальные значения; для этого возьмем от Ix1 или Iy1 первую производную по величины Ix1, Iy1 и Ix1y1 изменяются. Найдем значение угла, при котором Ix1 и Iy1 имеют экстремальные значения; для этого возьмем от Ix1 или Iy1 первую производную по 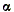 и преравняем ее нулю: и преравняем ее нулю:
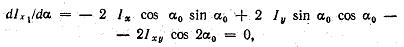
или
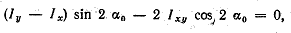
откуда
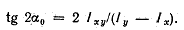 (1.28) (1.28)
Эта формула определяет положение двух осей, относительно одной из которых осевой момент инерции максимален, а относительно другой - минемален.
Такие оси называют главными. Моменты инерции относительно главных осей называются главными моментами инерции.
Значения главных моментов инерции найдем из формул (1.23) и (1.24), подставив в них 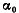 из формулы (1.28), при этом используем известные формулы тригонометрии для функций двойных углов. из формулы (1.28), при этом используем известные формулы тригонометрии для функций двойных углов.
После преобразований получим следующую формулу для определения главных моментов инерции:
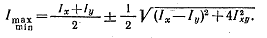 (1.29) (1.29)
Исследуя вторую производную 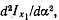 можно установить, что для данного случая (Ix < Iy) максимальный момент инерции Imax имеет место относительно главной оси, повернутой на угол можно установить, что для данного случая (Ix < Iy) максимальный момент инерции Imax имеет место относительно главной оси, повернутой на угол 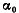 по отношению к оси х, а минимальный момент инерции - относительно другой, перпендикулярной оси. В большинстве случаев в этом исследовании нет надобности, так как по конфигурации сечений видно, какая из главных осей соответствует максимуму момента инерции. по отношению к оси х, а минимальный момент инерции - относительно другой, перпендикулярной оси. В большинстве случаев в этом исследовании нет надобности, так как по конфигурации сечений видно, какая из главных осей соответствует максимуму момента инерции.
Главные оси, проходящие через центр тяжести сечения, называются главными центральными осями.
Во многих случаях удается сразу определить положение главных центральных осей. Если фигура имеет ось симметрии, то она является одной из главных центральных осей, вторая проходит через центр тяжести сечения перпендикулярно первой. Сказанное следует из того обстоятельства, что относительно оси симметрии и любой оси, ей перпендикулярной, центробежный момент инерции равен нулю.
В случае если два главных центральных момента инерции сечения равны между собой, то у этого сечения любая центральная ось является главной, и все главные центральные моменты инерции одинаковы (круг, квадрат, шестиугольник, равносторонний шестиугольник).
Источник: http://sopromat.org | 





