Момент инерции сложной фигуры равен сумме моментов инерции ее составных частей
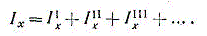 (1.20) (1.20)
Это непостредственно следует из свойств определенного инетеграла
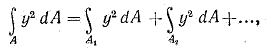
где А = А1 + А2 + ...
Таким образом, для вычисления момента инерции сложной фигуры надо разбить ее на ряд простых фигур, вычислить моменты инерции этих фигур и затем просуммировать эти моменты инерции.
Указанная теорема справедлива также и для центробежного момента инерции.
Моменты инерции прокатных сечений (двутавров, швеллеров, уголков и т.д.) приводятся в таблицах сортамента.
Источник: http://sopromat.org | 





