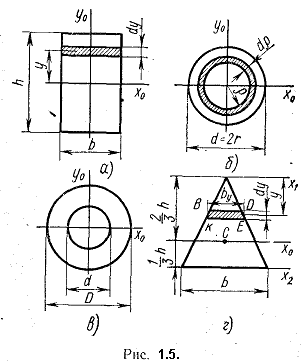
1. Прямоугольник (рис. 1.5,а). Вычислим момент инерции сечения относительно оси Х0, проходящей через центр тяжести параллельно основанию.
За dA примем площадь бесконечно тонкого слоя dA = bdy. Тогда
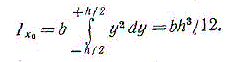
Итак,
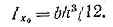 (1.11) (1.11)
Аналогично, получим
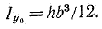 (1.12) (1.12)
2. Круг (рис. 1.5,б). Сначала определим полярный момент инерции относительно центра круга
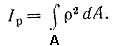
За dA принимаем площадь бесконечно тонкого кольца толщиной dp
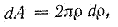
тогда
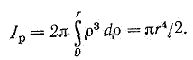
Следовательно,
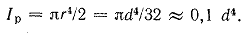 (1.13) (1.13)
Теперь легко найдем Ixo. Действительно, для круга согласно формуле (1.9.), имеем Iр = 2Iхо = 2Iуо, откуда
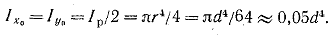 (1.14) (1.14)
2. Кольцо (рис. 1.5,в). Осевой момент инерции в этом случае равен разности моментов инерции внешнего и внутреннего кругов
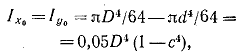 (1.15) (1.15)
где c = d/D.
Аналогично полярный момент инерции
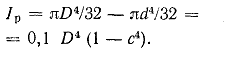 (1.16) (1.16)
2. Треугольник (рис. 1.5,г). Определим момент инерции относительно оси x1, параллельной основанию и проходящей через вершину треугольника
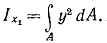
За dA примем площадь бесконечно тонкой трапеции KBDE, площадь которой можно считать равной площади прямоугольника:
dA = bydy,
где by - длина прямоугольника.
Легко получить из подобия треугольников
by = yb/h;
тогда
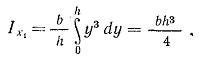 (1.17) (1.17)
Определим момент инерции относительно центральной оси; для этого используем формулу (1.10)
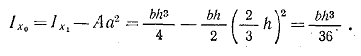 (1.18) (1.18)
Определим момент инерции относительно оси, проходящей через основание:
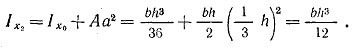 (1.19) (1.19)
Источник: http://sopromat.org | 





