Осевым, или экваториальным, моментом инерции сечения называется геометрическая характеристика, численно равная интегралу:
относительно оси х
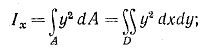 (1.6) (1.6)
относительно оси у
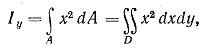
где у - расстояние от элементарной площадки dA до оси х (см. рис. 1.1.); х - расстояние от элементарной площадки dA до до оси у; D - область интегрирования.
Полярным моментом инерции сечения называется геометрическая характеристика, определяемая интегралом вида
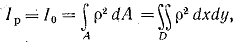 (1.7) (1.7)
где p - расстояние от площадки dA до точки (полюса) (см. рис. 1.1.) относительно которой вычисляется полярный момент инерции.
Осевой и полярный моменты инерции - величины всегда положительные.
Действительно, независимо от знака координаты произвольной площадки соответствующее слагаемое положительно, так как в него входит квадрат этой координаты.
Центробежным моментом инерции сечения называется геометрическая характеристика, определяемая интегралом вида
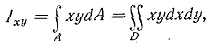 (1.8) (1.8)
где х,у - расстояния от площадки dA до осей x и y.
Моменты инерции измеряются в единицах длины в четвертой степени (по СИ - м^4, хотя для прокатных профилей по ГОСТу - см^4).
Центробежный момент инерции может быть положительным, отрицательным и, в частном случае, равным нулю.
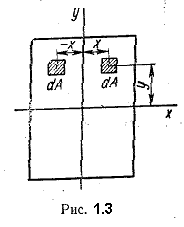
Если взаимно перпендикулярные оси х и у или одна из них являются осями симметрии фигуры, то относительно таких осей центробежный момент инерции равен нулю. Действительно, для симметричной фигуры всегда можно выделить два элемента ее площади (рис. 1.3.), которые имеют одинаковые ординаты у и равные, но противоположные по знаку абсциссы х. Составляя сумму произведений xydA для таких элементов, т.е. вычисляя интеграл (1.8.), получают в результате нуль.
Легко доказать, что полярный момент инерции относительно какой-либо точки равен сумме осевых моментов инерции относительно двух взаимно перпендикулярных осей, проходящих через эту точку.
Действительно, из рис. 1.1 видно, что
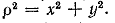
Подставив это значение p^2 в выражение (1.7.) получим
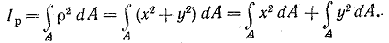
Следовательно, Ip = Ix + Iy.
Источник: http://sopromat.org | 





