Рассмотрим несколько примеров.

Пример 3.1. Определить опорные реакции консольной балки (рис. 3.3).

Решение. Реакцию заделки представляем в виде двух сил Az и Ay, направленных, как указано на чертеже, и реактивного момента MA.

Составляем уравнение равновесия балки.

1. Приравняем нулю сумму проекций на ось z всех сил, действующих на балку. Получаем Az = 0. При отсутствии горизонтальной нагрузки горизонтальная составляющая реакции равна нулю.

2. То же, на ось y: сумма сил равна нулю. Равномерно распределенную нагрузку q заменяем равнодействующей qaз, приложенной посредине участка aз:

Ay - F1 - qaз = 0,

откуда

Ay = F1 + qaз.

Вертикальная составляющая реакции в консольной балке равна сумме сил, приложенных к балке.

3. Составляем третье уравнение равновесия. Приравняем нулю сумму моментов всех сил относительно какой-нибудь точки, например относительно точки А:



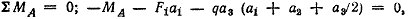
откуда





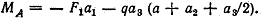
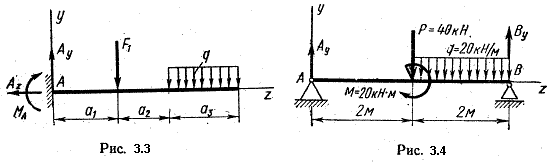
Знак минус показывает, что принятое вначале направление реактивного момента следует изменить на обратное. Итак, реактивный момент в заделке равен сумме моментов внешних сил относительно заделки.

Пример 3.2. Определить опорные реакции двухопорной балки (рис. 3.4). Такие балки обычно называют простыми.

Решение. Так как горизонтальная нагрузка отсутствует, то Az = 0

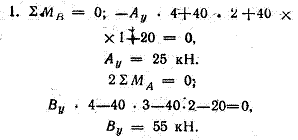
Вместо второго уравнения можно было использовать условие того, что сумма сил по оси Y равна нулю, которое ы данном случае следует применить для проверки решения:
25 - 40 - 40 + 55 = 0, т.е. тождество.

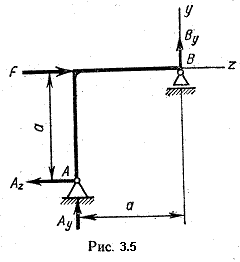
Пример 3.3. Определить реакции опор балки ломаного очертания (рис. 3.5).

Решение.

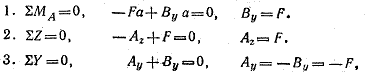
т.е. реакция Ay направлена не вверх, а вниз. Для проверки правильности решения можно использовать, например, условие того, что сумма моментов относительно точки В равна нулю.