При кручении, так же как и при растяжении, встречаются задачи, которые не могут быть решены с помощью одних только уравнений равновесия. В таких задачах количество неизвестных превышает число уранений равновесия. Порядок решения таких задач тот же самый, что и при решении статически неопределимых задач при растяжении (сжатии).
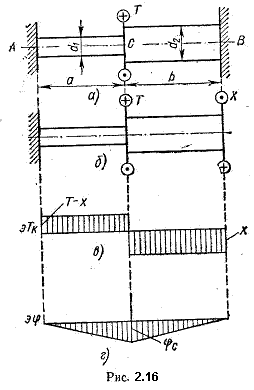
Рассмотрим для примера стержень с двумя заделанными концами (рис. 2.16, а). Такой стержень статически неопределим, так как для нахождения двух реактивных моментов, возникающих в заделках, статика дает лишь одно уравнение равновесия.
Отбросим одну заделку, заменив ее действие неизвестным моментом Х (рис. 2.15, б). Дополнительное уравнение (называемое, как известно, уранением деформации или уравнением перемещений) получим из условия, что угол поворота сечения у отброшенной заделки, равный углу закручивания стержня под действием моментов Т и Х, равен нулю (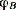 = 0). = 0).
В получившейся статически определимой системе, называемой основной системой, поворот сечения В происходит под действием внешнего момента и момента Х. Угол поворот сечения В под действием момента Х равен
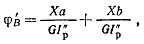
где 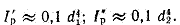
Угол поворота сечения В под действием момента Т равен
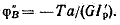
Подставляя эти значения и уравнение перемещений, получаем
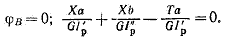
Отсюда определяем Х.
После этого можно определить крутящий момент в любом сечении и построить эпюру Тк и эпюру углов закручивания. Для построения эпюры 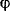 достаточно вычислить угол поворота сечения С. Он равен достаточно вычислить угол поворота сечения С. Он равен
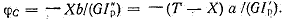
Углы поворота сечений А и В равны нулю, а так как угол поворота сечения линейно зависит от расстояния [см. формулу (2.19)], то полученные точки эпюры можно соединить прямыми линиями. Эпюры Тк и  представлены на рис. 2.16, в, г. представлены на рис. 2.16, в, г.
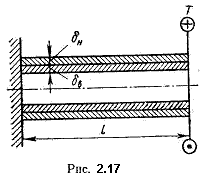
Пример 2.5. Тонкостенная трубка из материала с модулем Gв вставлена в другую с модулем Gн. Один конец получившейся конструкции заделан, а к другому приложен внешний момент Т, действующий на обе трубки (рис. 2.17). Определить крутящие моменты, возникающие в поперечных сечения трубок.
Решение. Неизвестных крутящих моментов два: во внутренней трубке Тк.в и в наружной трубке Тк.н.
Уравнение равновесия одно:
Тк.в + Тк.н = Т. (I)
Задача один раз статически неопределима. Составляем уранение деформаций, приравнивая между собой углы поворота сечений на правом конце трубок (равные полным углам закручивания трубок): 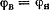
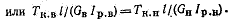 (II) (II)
Полярный момент инерции сечения внутренней трубки - Iр.в, наружной - Iр.н. Они определяются, как для кольцевых сечений, по формулам (см. здесь). При небольшой толщине стенок для вычисления углов закручивания можно пользоваться формулой (2.39 см. здесь), которая при постоянной толщине 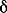 получает вид получает вид
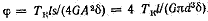 , ,
где d = (dн + dв)/2 - средний диаметр трубки; s = Пd - длина средней окружности сечения трубки.
Из двух уравнений (I) и (II) определяют крутящие моменты в поперечных сечениях трубок, а затем по формуле (2.37 см.здесь) - и напряжения. При значительной толщине стенок для определения напряжений следует пользоваться следующими формулами: см. здесь.
Источник: http://sopromat.org | 





