Значительно более жестким и поэтому более целесообразным при кручении являются тонкостенные стержни замкнутого профиля.
Рассмотрим цилиндрический стержень, поперечное сечение которого представлено на рис. 2.14. Толщину стенки 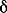 будем считать плавно изменяющейся вдоль линии контура, так что концентрацию напряжений можно не учитывать. будем считать плавно изменяющейся вдоль линии контура, так что концентрацию напряжений можно не учитывать.
Геометрическое место точек, равноотстоящих от внешнего и внутреннего контуров поперечного сечения, называется средней линией сечения.
Ввиду незначительной толщины стенки можно принять, что возникающие при кручении касательные напряжения будут равномерно распределены по толщине стенки и направлены по касательной к средней линии сечения.
Можно показать также, что произведение касательного напряжения в какой-либо точке стенки на ее толщину есть величина, постоянная для всех точек осевой линии контура сечения, т.е. 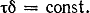
Для этого достаточно рассмотреть условие равновесия какого-либо элемента стержня, например элемента 1234 (рис. 2.14).
В продольном сечении 1-4 действует парное касательное напряжение 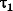 , в сечении 2-3 - парное касательное напряжение , в сечении 2-3 - парное касательное напряжение 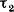
Спроектировав силы, действующие на элемент, на направление оси стержня, получим 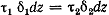 . .
Так как точки 3 и 4 взяты произвольно, то 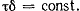
Теперь можно связать величину касательного напряжения с возникающим в сечении крутящим моментом.
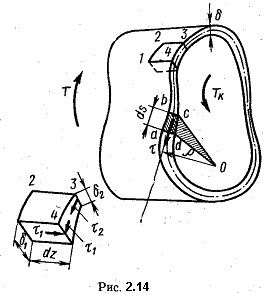
Сила, действующая на элементарную площадь 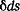 (рис. 2.14), равна, очевидно, (рис. 2.14), равна, очевидно, 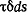 , а крутящий момент этой элементарной силы относительно произвольной точки О, лежащей в плоскости сечения, равен , а крутящий момент этой элементарной силы относительно произвольной точки О, лежащей в плоскости сечения, равен 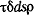 , относительно точки О. , относительно точки О.
Сумма моментов относительно оси, параллельной образующей стержня и проходящей через точку О, равна крутящему моменту
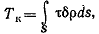
где интегрирование распространяется на всю длину контура s; но произведение pds равно удвоенной площади треугольника Oab; pds = 2dA. Следовательно, 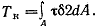
Произведение 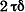 , как величину постоянную, можно вынести за знак интеграла. Под интегралом остается выражение , как величину постоянную, можно вынести за знак интеграла. Под интегралом остается выражение 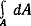 , что представляет собой площадь сплошного сечения, ограниченного средней линией сечения. , что представляет собой площадь сплошного сечения, ограниченного средней линией сечения.
Тогда
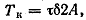 (2.36) (2.36)
откуда
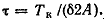 (2.37) (2.37)
Наибольшее напряжение будет в том месте, где толщина стенки минимальна
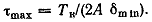 (2.38) (2.38)
Угол закручивания 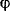 для стержня длиной l определим из условия, что работа внешнего скручивающего момента равна работе внутренних сил. Работа внешнего статически приложенного момента на угловом перемещении для стержня длиной l определим из условия, что работа внешнего скручивающего момента равна работе внутренних сил. Работа внешнего статически приложенного момента на угловом перемещении 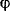 равна равна
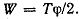
Вычислим теперь потенциальную энергию деформации, численно равную работе внутренних сил.
Потенциальная энергия для элемента объемом 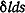 составит составит
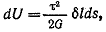
где l - длина стержня.
Полная потенциальная энергия энергия для всего стержня равна
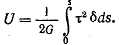
Интегрирование производится по длине s контура сечения.
Заменяя 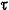 его значением из формулы (2.37), найдем его значением из формулы (2.37), найдем
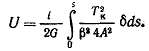
Вынесем постоянные величины за знак интеграла
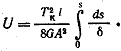
Учитывая, что потенциальная энергия U численно равна работе W внешнего момента, получим Тк = Т
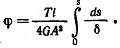 (2.39) (2.39)
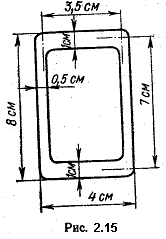
Пример 2.3. Определить наибоьльшее напряжение и угол закручивания трубчатого стержня (рис. 2.15), если Тк = Т = 1500 Н * м, G = 80000 МПа.
Решение. По формуле (2.38) находим
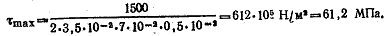
По формуле (2.39) определим угол закручивания на длине 1 м
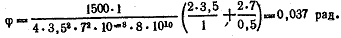
Пример 2.4. Определить наибольшее напряжение и угол закручивания того же стержня, если профиль будет открытым (т.е. если контур в одном месте будет разрезан).
Решение. Напряжение определяем по формуле (2.34):
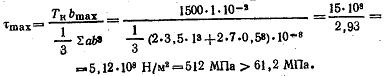
Заметим, что этот результат имеет смысл лишь для стержня, изготовленного из легированной стали, имеющей предел пропорциональности при чистом сдвиге 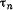 не ниже найденной величины не ниже найденной величины 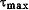 , так как все формулы настоящей главы справедливы лишь в пределах действия закона Гука. , так как все формулы настоящей главы справедливы лишь в пределах действия закона Гука.
Угол закручивания определяем по формуле (2.35)
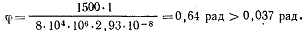
Сравнение результатов двух рассмотренных примеров подтверждает приемущества стержней замкнутого профиля по сравнению со стержнями открытого профиля при работе на кручение.
Источник: http://sopromat.org | 





